理解二分查找
二分查找用于在有序的列表中快速查询。虽然二分的思路很简单,但是要写出完全正确的二分查找代码,以及灵活使用二分查找解决问题,并不是那么简单。
之前在某个地方看到说,能一次性完全写对二分搜索的程序员寥寥无几。
本文将从分治开始,理解搜索区间,编写出正确的二分搜索代码。
从分治开始
Letcode704.二分查找是一道典型的二分题,题目要求为
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
二分查找的流程为
- 数组中排在中间的数字
nums[mid],与要找的数字target比较大小 - 因为数组是有序的,所以:
nums[mid] > target则说明要查找的数字应该从前半部分查找nums[mid] < target则说明应该从查找数字的后半部分查找nums[mid] === target则说明我们找到了目标元素,直接返回mid
- 这样不断查找缩小数量级(扔掉一半数据),直到找完数组为止
递归代码
如果我们要在一个无序的数组中找到某个元素,最简单的做法是遍历数组。思考一下,如果要使用递归该怎么写
当时数组长度为1时,我们可以直接得到答案;否则,我们每次都讲数组拆成两半,分别从左边和右边查找对应的数字
具体的代码类似下面
var search = function (nums, target) {
return dfs(0, nums.length - 1)
function dfs(l, r) {
// 当数组只有一个元素时,可以直接判断
if (l == r) {
return nums[l] === target ? l : -1
}
const mid = (l + r) >> 1
// 如果运气够好,可以直接返回mid
if(nums[mid] === target) return mid
// 是否在左边
let ans = dfs(l, mid)
if (ans !== -1) {
return ans
}
// 是否在右边
return dfs(mid + 1, r)
}
};这个代码本质上跟循环来查找元素没有任何区别,只是一个从中间开始,一个从最左边开始而已
for (let i = 0; i < nums.length; ++i) {
if (nums[i] === ans) {
return i
}
}但现在数组变成有序了,这个性质又什么特殊的呢?
顺序性非常有用,现在我们可以比较nums[target]的大小,选择是去左边找,还是右边找了。
var search = function (nums, target) {
return dfs(0, nums.length - 1)
function dfs(l, r) {
// 当数组只有一个元素时,可以直接判断
if (l == r) {
return nums[l] === target ? l : -1
}
const mid = (l + r) >> 1
if (nums[mid] === target) return mid
// 可以自己选择去左边还是右边,不需要两个都遍历了
if (nums[mid] > target) return dfs(l, mid - 1)
if (nums[mid] < target) return dfs(mid + 1, r)
}
};上面的代码可以进一步简化
var search = function (nums, target) {
return dfs(0, nums.length - 1)
function dfs(l, r) {
if (l > r) return -1
const mid = (l + r) >> 1
const val = nums[mid]
if (val === target) return mid
if (val > target) return dfs(l, mid - 1)
if (val < target) return dfs(mid + 1, r)
}
}dfs函数的两个参数代表我们要搜索的区间,通过与mid位置的元素对比,缩减搜索区间,最终返回结果。
递归函数可以让我们只专注于一次搜索的过程,更容易编写代码,在彻底理解了二分搜索的算法之后,我们再去编写循环形式的二分。
接下来我们看看二分搜索中的核心概念
搜索区间
在上面的递归函数dfs中,两个参数dfs(l, r)代表是是什么意思?
从字面意义上来看,搜索区间就是我们要搜索的某个子数组,在初始的时候,我们搜索的是整个数组;每个搜索的时候,会将搜索区间缩小一半的范围。
搜索区间的另外一个隐藏含义是:题目所求的目标元素所在的区间!我们为什么要不断缩小区间,就是为了最终定位到目标元素。
搜索什么时候终止?在上面的递归实现中,就是“递归函数什么时候终止”
- 一种情况是找到目标元素的时候,即
nums[mid] === target - 另外一种情况就是搜索区间为空的时候
那么搜索区间什么时候为空呢?这跟我们定义搜索区间的方式有关
- 左闭右闭,初始从
[0, n-1]开始,n表示搜索区间的子数组长度,当搜索区间[l, r]的l > r时,搜索区间就为空了 - 左闭右开,初始从
[0, n)开始,当搜索区间为[l, r)的l === r时,搜索区间就为空了
至于选择哪一种方式,没有啥优劣,哪种写法更符合你的思考习惯,就选择哪一种。
上面代码选择的是[l,r]左闭右闭的写法,所以后面的说明都是按照这种方式进行描述。
当搜索还没有终止的时候,我们需要通过二分来缩小搜索范围,由于nums[mid]已经进行了判断,所以剩下的搜索区间在[l,mid-1]和[mid+1,r]
val > target,目标元素在mid左侧,即搜索范围为[l,mid-1],递归调用dfs(l, mid-1)val < target,目标元素在mid右侧,即搜索范围为[mid+1,r],递归调用dfs(mid+1, r)
整个dfs函数的分治思路,就是通过不断缩小搜索范围,直到找到target,或者搜索范围为空。
我们也可以将上面的代码改成左闭右开的,那么初始的时候就是从dfs(0, nums.length)开始
var search = function (nums, target) {
return dfs(0, nums.length) // 这里变成了nums.length
function dfs(l, r) {
if (l === r) return -1 // 这里变成了相等,因为对于[l,r)来说,当l==r时即区间为空
const mid = (l + r) >> 1
const val = nums[mid]
if (val === target) return mid
if (val > target) return dfs(l, mid) // 由于是右开,这里变成了[l,mid)区间
if (val < target) return dfs(mid + 1, r) // 由于是左闭,这里还是[mid+1,r]区间
}
}几个细节问题
r初始值- 区间为空的判断是
l>r还是l===r - 左区间是
[l,mid]还是[l,mid+1]
这些问题都跟搜索区间的定义有关,只要想清楚了代码,你甚至也可以再改动一下代码,写出左开右开的代码
点击查看左开右开的代码
var search = function (nums, target) {
return dfs(-1, nums.length)
function dfs(l, r) {
if (l === r - 1) return -1
const mid = (l + r) >> 1
const val = nums[mid]
if (val === target) return mid
if (val > target) return dfs(l, mid)
if (val < target) return dfs(mid, r)
}
}循环写法
理解了上面的搜索区间,我们就可以将递归的二分写成循环的形式,循环是二分更常见的写法。
下面的代码依然采用左闭右闭定义的搜索区间
var search = function (nums, target) {
let l = 0
let r = nums.length - 1
while (l <= r) {
const mid = (l + r) >> 1
const val = nums[mid]
if (val === target) {
return mid
} else if (val > target) {
r = mid - 1
} else if (val < target) {
l = mid + 1
}
}
return -1
}这段代码,基本上是一比一还原的dfs函数,细小的区别在于
- 循环体内表示搜索的过程,因此循环体内的搜索区间肯定是有效的,因此while语句的条件是
l<=r,这在[l,r]左闭右闭区间内是一个有效的搜索区间 - 需要手动更新
l或者r,而不是像递归函数那样通过函数传参的形式更直观的展示更新后的搜索区间。
当然我们也可以编写左闭右开的区间
点我查看左闭右开的循环二分代码
var search = function (nums, target) {
let l = 0
let r = nums.length
while (l < r) {
const mid = (l + r) >> 1
const val = nums[mid]
if (val === target) {
return mid
} else if (val > target) {
r = mid
} else if (val < target) {
l = mid + 1
}
}
return -1
}再次强调一下:不需要刻意去背诵这些代码,到底是<还是<=、r是mid还是mid+1之类的细节,都是根据你定义的搜索区间来编写的,只要理解了搜索区间,编写这些代码就很轻松了。
在后面的章节中,我都会采用[l,r]的左闭右闭写法,不再单独强调。
找左右边界
排序数组中的数字可能重复,在某些时候需要找到某个数字的左边界或者右边界。
比如nums=[1, 2, 2, 3, 3, 5, 5],target=2时,数字2在数组中出现了多次,那么数字2的边界该怎么定义呢?
怎么定义边界
主流的编程语言提供了类似的API,我们先来看看他们的定义
lower_bound与upper_bound是C++的STL中,除了qsort之外唯二与算法相关的API
lower_bound所返回的是第一个大于或等于目标元素的元素地址upper_bound则是返回第一个大于目标元素的元素地
python的bisect也提供了bisect_left和bisect_right
bisect.bisect_left(a,x),在 a 中找到 x 合适的插入点以维持有序,如果 x 已经在 a 里存在,那么插入点会在已存在元素之前(也就是左边)bisect.bisect_right(a,x),与bisect_left类似,但返回的插入点是 a 中已存在元素 x 的右侧
import bisect
# 定义有序数组
nums = [1, 2, 2, 3, 3, 5, 5]
target = 2
# 使用 bisect_left 查找目标值的左边界
lower_index = bisect.bisect_left(nums, target)
# 使用 bisect_right 查找目标值的右边界
upper_index = bisect.bisect_right(nums, target)
# 输出结果
print(f"bisect_left index: {lower_index}")
print(f"bisect_right index: {upper_index}")返回的bisect_left index为1,而bisect_right为3
不论是C++还是Python,都采用了左闭右开的方式,来定义数组中某个元素的边界,即数字2在nums=[1, 2, 2, 3, 3, 5, 5]的边界是[1,3)。
下文也将按照左闭右开的定义,通过二分来查询目标数字的左右边界。
- 左边界,第一个大于等于目标数字的元素索引值
- 右边界,第一个大于目标数字的元素索引值
查找左边界
我们先来看看查找左侧边界的情况。先只考虑target必定出现在nums中的情况,这样会简单一点。
还是搜索区间
首先我们确定搜索范围还是[0, n - 1],这样循环的条件就是while(l <= r),然后二分找到中间索引值
当nums[mid] > target时,目标肯定在左边,因此搜索范围缩小为[l, mid-1],更新r = mid - 1
当nums[mid] < target时,目标肯定在右边,因此搜索范围缩小为[mid+1, r],更新l = mid + 1
当nums[mid] == target时,有两种情况
- mid左边还有值为target的元素,目标值的在
[l, mid - 1] - mid左边没有值为target的元素,mid就是我们要求的目标值
但搜索还没结束,我们并不知道左边还有没有target的值,因此还需要继续搜索。由于寻找搜索范围的是target的左边界,我们还需要搜索[l, mid-1]的区间,因此需要更新r = mid - 1
你也许会有疑问,在nums[mid] == target的情况下,搜索区间更新为[l, mid-1],如果这个时候mid的左边并没有有值为target的元素,那不是就找不到目标值了吗?
无需担心,如果左边没有target,那么说明后续的循环中nums[mid]都是比target更小的,都会更新l = mid + 1,l最终还是会向右移动到nums[mid]===target的这个mid的位置。
反复上面的搜索,直到最后搜索区间为空,即l > r。
返回哪个值
最后一个问题,我们上面的一通搜索操作,最后应该返回什么值呢?l还是r?
由于在每次搜索条件中,如果nums[mid]大于target,我们就会将r左移;而当nums[mid]小于target,我们都会将l右移,这样做的结果是什么?l和r都会向target靠近!
由于我们现在只考虑target必定出现在nums中的情况,则在最后一次的搜索区间[l,r],此时l==r,搜索区间长度为1,对于这个元素last,距离target只有一步之遥:要么小于target,要么等于target
- 如果
last === target,那么r最终会变成l-1,l还是指向last,也就是等于target的元素 - 如果
last < target,那么l最终会变成mid+1,最终还是会指向等于target的元素
可以看出,在搜索结束后,r指针指向的数字肯定是小于target的,l指针指向的数字肯定是等于target的元素,所以l符合我们对于左边界的定义,因此函数返回l即可。
如果你对这个过程还有些困惑,可以参考下面的图示模拟一下整个过程

代码实现
完整的leftBound代码实现
function leftBound(nums, target) {
let l = 0
let r = nums.length - 1
while (l <= r) {
const mid = (l + r) >> 1
if (nums[mid] === target) {
r = mid - 1
} else if (nums[mid] > target) {
r = mid - 1
} else if (nums[mid] < target) {
l = mid + 1
}
}
return l
}
var nums = [1, 2, 2, 3, 3, 5, 5], target = 2 // 1
var ans = leftBound(nums, target)
console.log(ans)整理一下二分找左边界的代码模版
- 确定查询范围是
[0, n-1] - 当
nums[mid] >= target时,r = mid - 1 - 当
nums[mid] < target时,l = mid + 1 l > r时跳出循环,最后返回l
同样不建议大家死记硬背这个模版,而是在理解搜索区间的基础上,自己可以把这个代码写出来。
相关题目练习
target不存在
在前面我们设定了target必定出现在nums中,试想一下,如果target不存在时,leftBound返回的值是什么?
或者说,最后一轮的搜索区间的[l,r]是否有特殊的含义?
还是用上面的nums=[1, 2, 2, 3, 3, 5, 5],target=4例子,
- 第一轮搜索区间
[0,6],mid为3,nums[mid]<4,所以更新l为mid+1 - 第二轮搜索区间
[4,6],mid为5,nums[mid]>4,所以更新r为mid-1 - 第三轮搜索区间
[4,4],mid为4,nums[mid]<4,所以更新l为mid+1 - 第四轮搜索区间
[5,4],搜索区间为空,退出循环
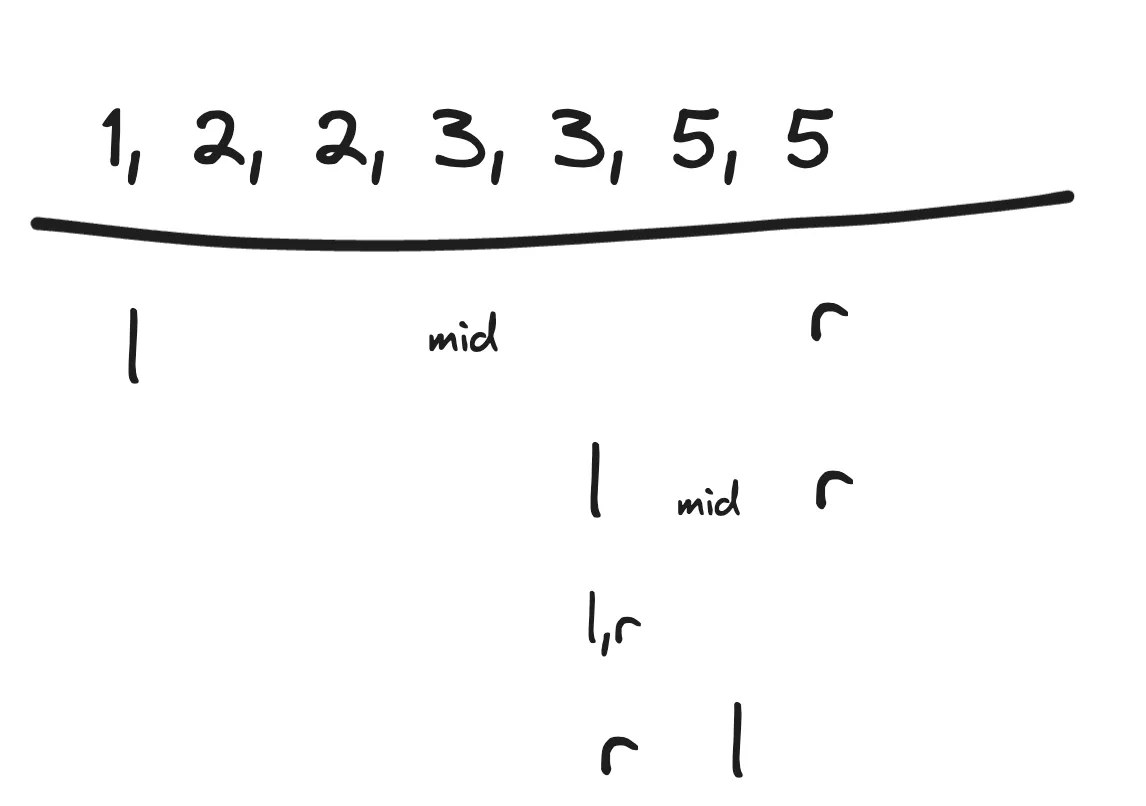
所以,在循环结束后
l对应的元素是数组中第一个大于target的元素索引值(因为l最后有可能为n,该值可能不存在)r对应的元素是数组中第一个小于target的元素索引值(因为r最后有可能为-1,该值可能不存在)
因此,leftBound返回值l,实际上是返回有序数组中第一个大于或等于target的数字索引值(这正符合左边界的定义);如果l===n,则说明数组中不存在这种数字
找到右边界
找右边界与找左边界的逻辑十分相似。
还是nums=[1, 2, 2, 3, 3, 5, 5],target=2为例子,根据左闭右开的右边界定义,期望返回的结果是3
我们的搜索区间还是采用左闭右闭,从[0,n-1]开始搜索,循环条件为while(l <= r)
当nums[mid] < target,搜索区间缩小为[mid+1, r]
当nums[mid] > target,搜索区间缩小为[l, mid-1]
当nums[mid] === target时,由于查找的是右边界,因此还是需要在右边的区间继续搜索,因此搜索区间为[mid+1,r]
当l>r时,循环结束,此时l 指向的就是右边界,返回l即可
function rightBound(nums, target) {
let l = 0
let r = nums.length - 1
while (l <= r) {
const mid = (l + r) >> 1
if (nums[mid] === target) {
l = mid + 1
}else if (nums[mid] < target) {
l = mid + 1
} else {
r = mid - 1
}
}
return l
}同理,如果数组元素中不存在target,循环结束之后,l是第一个比target大的数字的索引值,r是最后一个比target小的数字的索引值。
隐藏的二分题
如果是有序数组查找数字或者边界,大概率可以使用二分。
但是有一些题目,从题目要求上并不能直观地看出是否可以使用二分,下面整理了一些这种题目
排序数组旋转
排序数组旋转的意思是对于一个有序的数组,在某个索引值进行旋转,变成两段有序的数组,比如[0,1,2,4,5,6,7]会在下边3处旋转,会变成[4,5,6,7,0,1,2]。对于这种数组,如何找到其中的最小值呢?或者说找到那个旋转点呢?
排序数组旋转是比较经典的二分题,需要对搜索区间有比较深刻的认识
首先看看153这道题,限定了数组中没有重复的数字,来看看怎么通过搜索区间处理。
首先,我们初始化搜索区间还是[0, n-1]。
对于中间节点nums[mid],
- 如果
nums[mid] > nums[r]说明目标在右边,更新搜索区间为[mid+ 1, r]。 - 如果
nums[mid] < nums[r]说明右侧数组是升序的,目标在左边,因为mid对应的数字有可能就是最小值,不能将mid排除在搜索区间外,所以更新搜索区间为[l,mid]
最后搜索区间只存在一个元素,循环退出,这个元素就是我们要找的最小值,直接返回nums[l]
var findMin = function (nums) {
let l = 0
let r = nums.length - 1
// 搜索区间至少要2个元素,才可以比较
while (l < r) {
const mid = (l + r) >> 1
if (nums[mid] > nums[r]) {
l = mid + 1
} else if (nums[mid] < nums[r]) {
r = mid
}
// 由于数组没有重复的数字,不用处理nums[mid] === nums[r]的情况
}
return nums[l]
}154这道题在153题的基础上,增加了数组可能有重复数字的条件。
直接用上面的代码,当nums[mid] === nums[r]的时候,就会出现死循环,因为这个上面的代码在这种情况下没有更新搜索区间。
那么,在这种情况下,应该如何更新搜索区间呢?
当nums[mid]和nums[r]相等时,无法确定最小值的确切位置,比如[3,1,3,3,3]这种测试用例。
在这种情况下,为了缩小搜索区间避免死循环,我们可以将r减1。
这样,即可以减小搜索区间,又可以避免将正确答案排除的情况,因为nums[mid]和nums[r]相等,即使nums[r]对应的就是最小值,最后也可以收敛到nums[mid],所以绝对不会错过正确答案。
var findMin = function (nums) {
let l = 0
let r = nums.length - 1
while (l < r) {
const mid = (l + r) >> 1
if (nums[mid] > nums[r]) { // 最小值在右半部分
l = mid + 1
} else if (nums[mid] < nums[r]) { // 最小值在左半部分或者就是mid
r = mid
} else {
// 当nums[mid]和nums[r]相等时,无法确定最小值的确切位置
// 即使nums[r]是最小的元素,也可以将其减1,缩小搜索范围,因为nums[mid]和nums[r]这个时候是相等的
r--
}
}
return nums[l];
}33题就是154题的基础上再进行一次二分,这里不在展开。
二分搜索的难点在于定义搜索区间,以及在每轮搜索中如何缩小搜索区间,通过这几道题目的练习,对搜索区间的重要性应该有比较深刻的理解了。
求极值
有一批答案都符合要求,要找最小值/最大值,实际上也可以转成求边界的问题。
比如875. 爱吃香蕉的珂珂这道题
珂珂喜欢吃香蕉。这里有
n堆香蕉,第i堆中有piles[i]根香蕉。警卫已经离开了,将在h小时后回来。珂珂可以决定她吃香蕉的速度
k(单位:根/小时)。每个小时,她将会选择一堆香蕉,从中吃掉k根。如果这堆香蕉少于k根,她将吃掉这堆的所有香蕉,然后这一小时内不会再吃更多的香蕉。珂珂喜欢慢慢吃,但仍然想在警卫回来前吃掉所有的香蕉。
返回她可以在
h小时内吃掉所有香蕉的最小速度k(k为整数)。其中
piles.length <= h <= 109
根据题意,我们可以列出下面的公式
let ans = 0
for(const num of piles){
ans += Math.ceil(num / k)
}要求满足ans<=h时k的最小值,最极端情况就是每次都吃完一堆,这样ans就为piles.length,所以k的最大值就是Math.max(...piles)。
题目要求k的最小值,我们就可以在[1,max]的范围内进行二分,因为max肯定是满足的,需要向左找最小值,所以就变成了一个求左边界的问题。
完整代码如下
var minEatingSpeed = function (piles, H) {
const max = Math.max(...piles)
let l = 1
let r = max
while (l <= r) {
const mid = (l + r) >> 1
const val = clac(mid)
if (val > H) {
// 说明速度太小,需要右移
l = mid + 1
} else {
r = mid - 1
}
}
return l
function clac(k) {
let ans = 0
for (const num of piles) {
ans += Math.ceil(num / k)
}
return ans
}
}题目475. 供暖器也是类似的思路,首先确定取值范围,然后求左边界
var findRadius = function (houses, heaters) {
houses.sort((a, b) => a - b)
heaters.sort((a, b) => a - b)
// 确定目标值的最大值,一个加热器可以覆盖所有的房间
const max = Math.max(Math.abs(heaters[heaters.length - 1] - houses[0]), Math.abs(heaters[0] - houses[houses.length - 1]))
let l = 0 // 由于加热器可以与房间重叠,所以最小值是0
let r = max
while (l <= r) {
const mid = (l + r) >> 1
if (check(mid)) {
r = mid - 1
} else {
l = mid + 1
}
}
function check(radius) {
//...
}
}这个check函数怎么写呢?只需要遍历房间列表,找到与之最近的那个加热器看看距离是否小于radius,如果所有房间都能找到这样的加热器,就说明radius满足条件。
由于heaters是我们排过序的,所以可以继续用二分在有序数组中找到符合条件的目标值
function check(radius) {
for (const house of houses) {
//对于每个房间,二分找到其最近的那个加热器,看看能否满足条件
let l = 0
let r = heaters.length - 1
let flag = false
while (l <= r) {
const mid = (l + r) >> 1
if (Math.abs(heaters[mid] - house) <= radius) {
flag = true
break
} else if (heaters[mid] > house) {
r = mid - 1
} else if (heaters[mid] < house) {
l = mid + 1
}
}
if (!flag) return false
}
return true
}这样,整个代码在两个地方使用了二分,可以很快速地求到答案。
类似的用二分求极值的题目还有
点击查看代码
// 答案在[0,max(grid)]中间,因此可以使用二分,找到左边界
var swimInWater = function (grid) {
let max = 0
const n = grid.length
for (let i = 0; i < n; ++i) {
for (let j = 0; j < n; ++j) {
max = Math.max(max, grid[i][j])
}
}
let l = 0
let r = max
while (l <= r) {
const mid = (l + r) >> 1
const visited = {}
if (move(0, 0, mid, visited)) {
// 可以到达,答案在[l,mid]中间
r = mid - 1
} else {
// 不能到达,答案在[mid+1,r]中间
l = mid + 1
}
}
return l
function move(i, j, t, visited) {
if (i < 0 || i == n || j < 0 || j == n) return false
if (grid[i][j] > t) {
return false
}
if (i === n - 1 && j === n - 1) return true
const key = `${i},${j}`
if (visited[key]) return false
visited[key] = 1
return move(i, j + 1, t, visited) || move(i, j - 1, t, visited) || move(i + 1, j, t, visited) || move(i - 1, j, t, visited)
}
}点击查看代码
// 答案在[0,max(abs(heights))]之间,所以可以用二分
var minimumEffortPath = function (heights) {
let max = 0
let min = Infinity
const m = heights.length
const n = heights[0].length
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
max = Math.max(max, heights[i][j])
min = Math.min(min, heights[i][j])
}
}
let l = 0
let r = Math.max(max - heights[0][0], heights[0][0] - min)
while (l <= r) {
const mid = (l + r) >> 1
if (check(mid)) {
r = mid - 1
} else {
l = mid + 1
}
}
return l
function check(limit) {
const visited = new Array(m).fill(0).map(() => new Array(n).fill(0))
let queue = [[0, 0]]
visited[0][0] = 1
// bfs,将符合条件的路径加入,看看最后是否能到左下角
while (queue.length) {
const arr = []
for (const [i, j] of queue) {
if (i === m - 1 && j === n - 1) {
return true
}
const cur = heights[i][j]
enqueue(arr, cur, i + 1, j)
enqueue(arr, cur, i - 1, j)
enqueue(arr, cur, i, j + 1)
enqueue(arr, cur, i, j - 1)
}
queue = arr
}
return false
function enqueue(arr, prev, i, j) {
if (i < 0 || i === m || j < 0 || j === n) return
if (visited[i][j]) return
const cur = heights[i][j]
if (Math.abs(prev - cur) > limit) return
visited[i][j] = 1
arr.push([i, j])
}
}
}其他
如果数组中不存在负数,那么其前缀和也肯定是升序的,在某些特殊的问题中,也可以使用二分处理。
此外,数组的索引值也是升序的,也可以用来处理某些特定题目,比如2055. 蜡烛之间的盘子
有时间再补充相关的题目内容
小结
二分查找还有一些细节,比如为了l+r过大,导致避免mid溢出,可以下面这种方式求中间索引值
const mid = l + (r - l) >>1这些细节对于二分查找的核心概念没有多少影响,面对用例时按需处理即可。
二分查找最重要的是确定搜索区间,以及如何缩小区间,这两点清楚了,二分代码就容易写出来了。
你要请我喝一杯奶茶?
版权声明:自由转载-非商用-保持署名和原文链接。
本站文章均为本人原创,参考文章我都会在文中进行声明,也请您转载时附上署名。
