初识并查集
并查集可以快速检测两个节点是否连通(具有相同的父节点),虽然用邻接矩阵也可以实现,但并查集空间复杂度是O(n),且时间复杂度也可以接近O(1),在处理图中某些特定问题非常有用。
参考:
并查集有两个操作
- union 将两个节点连接
- find, 查询两个节点是否连通
基础实现
首先实现一个parent数组,在初始化阶段,每个节点都是独立的,每个元素i对应的parent[i]都是他自己
class DisjointSet {
constructor(size) {
this.parent = new Array(size).fill(0)
for (let i = 0; i < size; ++i) {
this.parent[i] = i
}
}
}然后我们需要实现一个find函数,该函数用来寻找某个节点的根节点,我们可以通过parent数组向上,找到根节点,根节点的特征是praent[i]===i,查找操作是并查集中最频繁的操作(从名字上就可以看出来)
find(x) {
while (this.parent[x] !== x) {
x = this.parent[x]
}
return x
}然后实现一个union方法,可以将两个节点关联起来。
关联的定义是:两个节点只要有相同的根节点,那么他们就是关联的
因此,最简单的就是修改某个元素的parent[i],如果两个节点本身就在一颗树里面,就不做任何事情
union(x, y) {
const rx = this.find(x)
const ry = this.find(y)
if (rx === ry) return
this.parent[ry] = rx
}然后我们就可以判断两个节点是否关联了
connected(x, y) {
return this.find(x) === this.find(y)
}现在,我们实现了一个最基本的并查集
const set = new DisjointSet(5)
set.union(0, 1)
set.union(1, 2)
console.log(set.connected(0, 2)) // true如果要找到最终形成了多少堆数据,可以遍历parent数组,当parent[i]===i时,将计数器加1即可
let cnt = 0
for(let i = 0; i < n; ++i){
if(this.find(i) === i){
cnt++
}
}优化
上面的代码中,在极端情况下,find的时间复杂度是O(n),因此需要优化。
按数量合并
可以看出,树的层级越深,需要的查询次数越多。从代码中可以看出,影响树的层级主要是在union方法中
this.parent[ry] = rx简单粗暴地将两个树进行了关联
看一下下面的示例,有1和2两个根节点,1树种共有4个节点,2树种共有2个节点,现在需要将1和2关联起来 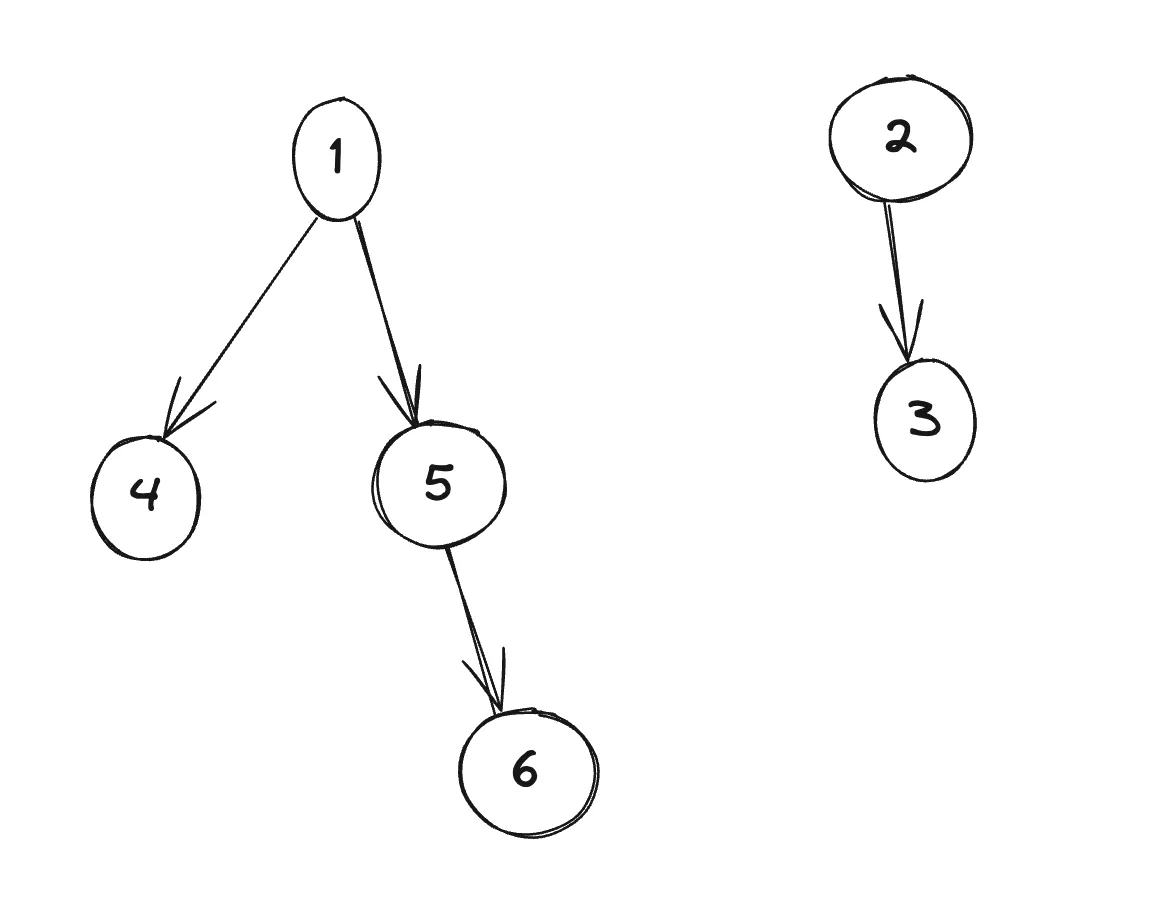
是将1作为2的子节点
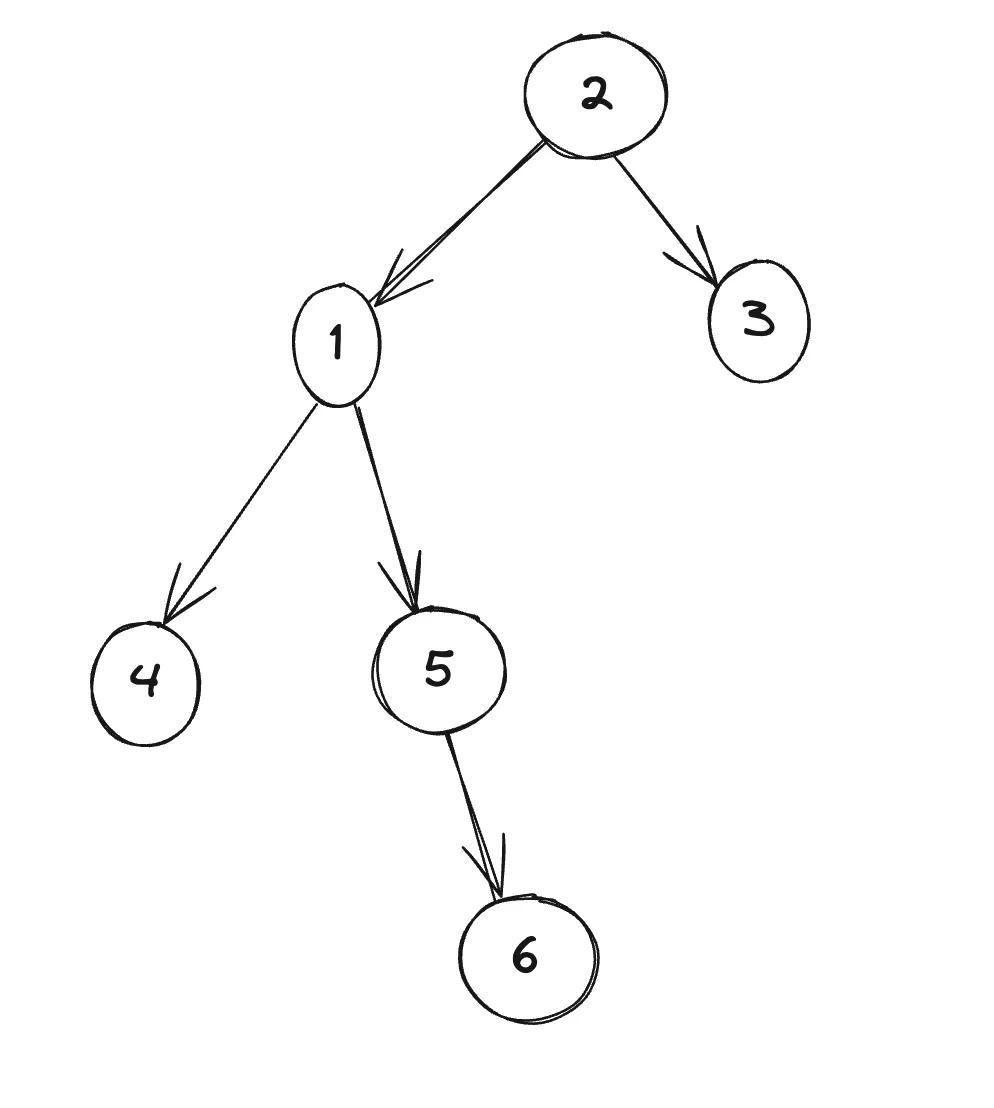
还是将2作为1的子节点
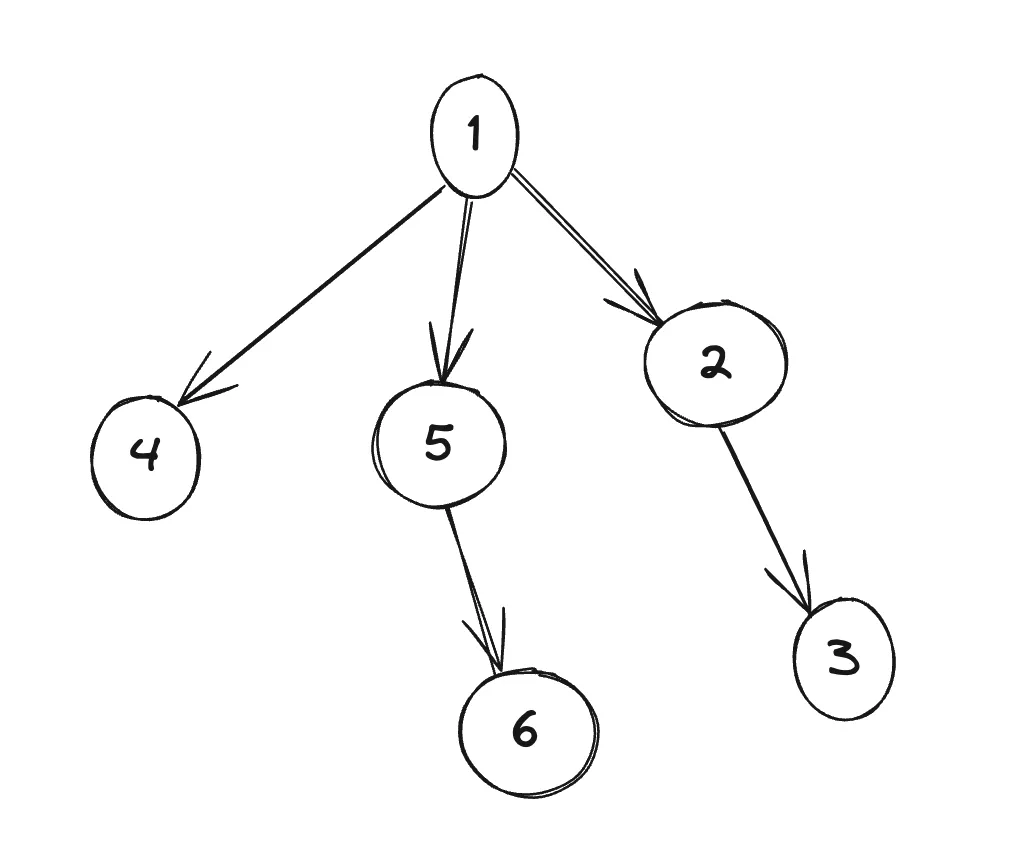
将节点树更小的树,放在节点树更大的树下面,整个树会更加平衡,对于相同数量的节点而言,平衡树的层级会更低。
因此,我们可以使用一个单独的size数组,保存每个根节点的数量,这样在union的时候,就可以选择合并后的根节点
class DisjointSet {
constructor(size) {
this.parent = new Array(size).fill(0)
this.size = new Array(size).fill(0)
for (let i = 0; i < size; ++i) {
this.parent[i] = i
this.size[i] = 1
}
}
union(x, y) {
const rx = this.find(x)
const ry = this.find(y)
if (rx === ry) return
const sx = this.size[rx]
const sy = this.size[ry]
if (sy > sx) {
// y作为根节点
this.parent[rx] = ry
this.size[ry] += sx
} else {
// x作为根节点
this.parent[ry] = rx
this.size[rx] += sy
}
}
// ...
}按秩合并
上面是按照节点的数量来选择合并的根节点。由于影响查询效率的是树的高度,因此,另外一种合并方法是按照树的高度来进行合并:将较矮的树合并到较高的树里面。在这个过程中,树的高度也被称作秩,”秩“的定义如下:
- 只有根节点的树(即只有一个元素的集合),秩为0;
- 当两棵秩不同的树合并后,新的树的秩为原来两棵树的秩的较大者;
- 当两棵秩相同的树合并后,新的树的秩为原来的树的秩加一。
只需要稍微改一下上面的代码,变成rank数组,就可以实现
constructor(size) {
this.parent = new Array(size).fill(0)
this.rank = new Array(size).fill(0)
for (let i = 0; i < size; ++i) {
this.parent[i] = i
this.rank[i] = 1
}
}
union(x, y) {
const rx = this.find(x)
const ry = this.find(y)
if (rx === ry) return
if (this.rank[ry] > this.rank[rx]) {
this.parent[rx] = ry
} else {
this.parent[ry] = rx
if (this.rank[ry] === this.rank[rx]) {
this.rank[rx] += 1
}
}
}按秩合并可以可以减少查询的路径长度,提升效率
路径压缩
在并查集中,我们实际上只关心某个节点与其根节点,中间的父节点并没有啥作用,因此,在find某个节点的时候,我们可以使用路径压缩。
所谓路径压缩,其实就是在找到某个节点的根节点之后,将其直接挪动到根节点的下面,这样下次寻找的时候,只需要查询1次就可以找到根节点了。
find(x) {
let i = x
while (this.parent[x] !== x) {
x = this.parent[x]
}
this.parent[i] = x
return x
}还有一些路径压缩算法,在while循环的过程中,提前将x的路径父节点也进行更新,这样可以减少部分节点查询的耗时。
const parent = this.parent
while (parent[x] != x) {
// 进行路径压缩
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;在路径合并中,节点的路径会缩短,这可能会导致根节点的高度缩短,在这种情况下,是否需要准确更新根节点的秩?
答案是:不需要。
在路径压缩的过程中,树的高度已经被减小到了极低的水平,根节点的秩通常不再是一个影响并查集性能的关键因素。
秩的作用主要是用来决定合并时将哪个树作为另一个树的子树,以保持树的平衡。而维护根节点秩的代价会高于收益,因为需要遍历整个树来计算新的高度。
相关题目
你要请我喝一杯奶茶?
版权声明:自由转载-非商用-保持署名和原文链接。
本站文章均为本人原创,参考文章我都会在文中进行声明,也请您转载时附上署名。
