snabbdom源码解析

发布于 2021-04-11 13:11:13| 分类于 源码分析/diff算法

最新在梳理一些前端框架的核心实现，关于diff算法这一块，发现目前大部分文章都是将源码翻译一遍，而关于诸如“为啥要定义多个游标”、”首尾对比”等细节，并没有给出比较好的解释。因此打算整理snabbdom源码，同时回答前面提到的一些问题。

如果只关心diff算法的核心实现，可以直接跳转到 patchVnode diff新旧节点这一章节

使用流程

parcel搭建开发环境

由于仓库并没有提供类似于dev之类的开发环境，可以使用Pracel快速搭建一个

首先克隆仓库，执行npm install && npm run build进行打包

然后在项目examples目录下创建一个demo目录，新建index.js和index.html

// index.html
<button id="change">change</button>
<div id="container"></div>
<script src="./index.js"></script>

import { init, classModule, propsModule, styleModule, eventListenersModule, h } from "../../build/index";

const patch = init([
  classModule, // makes it easy to toggle classes
  propsModule, // for setting properties on DOM elements
  styleModule, // handles styling on elements with support for animations
  eventListenersModule // attaches event listeners
]);

const container = document.getElementById("container");

const renderItem = (item)=>{
  return h("div", {key:item}, item);
}
const oldList = ["A", "B", "C", "D", "E"].map(renderItem);
const newList = ["B", "A", "C", "F", "G", "D"].map(renderItem);
const vnode = h("div", {}, oldList);
patch(container, vnode);

document.getElementById("change").onclick = ()=>{
  const newVnode = h("div", {}, newList);
  patch(vnode, newVnode);
}

然后在examples/demo目录下启动parcel index.html即可。

相关概念

snabbdom只提供了几个基础接口，使用起来大概是下面的流程，

• 使用init和内置模块初始patch方法
• 使用h方法创建vnode
• 初始化patch(container, vnode)，container为应用根节点
• 更新path(vnode, newVnode)

vnode就是一个JS对象，用来描述真实的DOM，包含一些主要的信息

export interface VNode {
  sel: string | undefined; // 用来区分不同类型的节点
  data: VNodeData | undefined; // 配置数据，可以携带一些钩子或其他信息
  children: Array<VNode | string> | undefined; // 子节点
  elm: Node | undefined; // 对应的DOM实例
  text: string | undefined; // 文本
  key: Key | undefined; // key，在兄弟节点中的唯一标识
}

h方法的作用就是根据sel、data和children返回一个vnode

export function h(
  sel: string,
  data: VNodeData | null,
  children: VNodeChildren
): VNode

patch方法通过init方法构建，是整个框架的核心，也是本文关注的重点

patch 入口收敛

先说流程

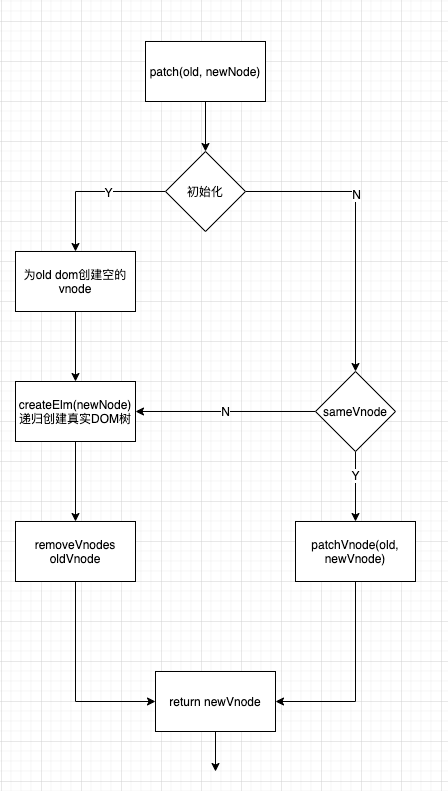
• 首先判断oldVnode是否是vnode，
  • 如果不是，则说明是初始化，传入的一个container DOM节点，使用该dom节点创建一个empty vnode，作为oldVnode
• 通过sameVnode新旧vnode是否相同
  • 如果不是，则通过createElm(newVnode)前序遍历虚拟dom树构建真实DOM树，然后将传入的container DOM替换成新的DOM
  • 如果是，则说明newVnode可以复用oldVnode的DOM实例，vnode.elm = oldVnode.elm，然后走patchVnode流程

再看代码，由于insert的钩子需要等到节点被插入到dom中才会被调用，因此使用了一个insertedVnodeQueue列表，在遍历树的时候收集所有被插入的vnode

  function patch(oldVnode: VNode | Element, vnode: VNode): VNode {
    let i: number, elm: Node, parent: Node;
    const insertedVnodeQueue: VNodeQueue = [];
    for (i = 0; i < cbs.pre.length; ++i) cbs.pre[i]();

    if (!isVnode(oldVnode)) {
      oldVnode = emptyNodeAt(oldVnode);
    }

    if (sameVnode(oldVnode, vnode)) {
      patchVnode(oldVnode, vnode, insertedVnodeQueue);
    } else {
      elm = oldVnode.elm!;
      parent = api.parentNode(elm) as Node;

      // 根据vnode初始化DOM树
      createElm(vnode, insertedVnodeQueue);

      if (parent !== null) {
        api.insertBefore(parent, vnode.elm!, api.nextSibling(elm));
        // 里面会完成对oldVnode dom实例的移除
        removeVnodes(parent, [oldVnode], 0, 0);
      }
    }

    for (i = 0; i < insertedVnodeQueue.length; ++i) {
      insertedVnodeQueue[i].data!.hook!.insert!(insertedVnodeQueue[i]);
    }
    for (i = 0; i < cbs.post.length; ++i) cbs.post[i]();
    return vnode;
  };

这样我们就可以从两条路createElm和patchVnode分别出发，看看初始化和更新时的差异

snabbdom使用了与C语言类似的编程习惯，会在函数头部声明变量，在后续的代码中只进行赋值

createElm 递归创建DOM树

主要功能是根据vnode的sel创建DOM节点，如果有子节点，则进行前序遍历，递归调用createElm获取子节点对应的DOM节点，然后将其插入到父DOM节点

可以看出，这里是在递归的同时就执行创建DOM的操作，为了方便阅读，下面的源码进行了删减

  function createElm(vnode: VNode, insertedVnodeQueue: VNodeQueue): Node {
    let i: any;
    let data = vnode.data;
    const children = vnode.children;
    const sel = vnode.sel;
    if (sel === "!") {
      if (isUndef(vnode.text)) {
        vnode.text = "";
      }
      vnode.elm = api.createComment(vnode.text!);
    } else if (sel !== undefined) {
      // 根据sel解析tag
      const elm = (vnode.elm =
        isDef(data) && isDef((i = data.ns))
          ? api.createElementNS(i, tag, data)
          : api.createElement(tag, data));
			// 递归创建子节点
      if (is.array(children)) {
        for (i = 0; i < children.length; ++i) {
          const ch = children[i];
          if (ch != null) {
            // 同时将子节点对应的DOM添加到父DOM
            api.appendChild(elm, createElm(ch as VNode, insertedVnodeQueue));
          }
        }
      } else if (is.primitive(vnode.text)) {
        api.appendChild(elm, api.createTextNode(vnode.text));
      }
    } else {
      vnode.elm = api.createTextNode(vnode.text!);
    }
    return vnode.elm;
  }

这样，就根据一个vnode得到了它对应的完整DOM树。

patchVnode diff新旧节点

前面提到，当新旧节点类型相同时，就会进入patchVnode流程，主要进行新旧节点对应子节点列表的判断

function patchVnode(
  oldVnode: VNode,
  vnode: VNode,
  insertedVnodeQueue: VNodeQueue
) {

  const elm = (vnode.elm = oldVnode.elm)!;
  const oldCh = oldVnode.children as VNode[];
  const ch = vnode.children as VNode[];
  // 节点在内存相同，则不进行比较
  if (oldVnode === vnode) return;

  if (isUndef(vnode.text)) {
    if (isDef(oldCh) && isDef(ch)) {
      // 同时存在新旧子节点，如果子节点在内存相同，则不进行比较
      if (oldCh !== ch) updateChildren(elm, oldCh, ch, insertedVnodeQueue);
    } else if (isDef(ch)) {
      // 如果只存在新节点，则说明全部为新增节点，判断一下之前是否为文本节点
      if (isDef(oldVnode.text)) api.setTextContent(elm, "");
      // 然后插入新节点
      addVnodes(elm, null, ch, 0, ch.length - 1, insertedVnodeQueue);
    } else if (isDef(oldCh)) {
      // 如果只存在旧节点，则需要全部移除
      removeVnodes(elm, oldCh, 0, oldCh.length - 1);
    } else if (isDef(oldVnode.text)) {
      api.setTextContent(elm, "");
    }
  } else if (oldVnode.text !== vnode.text) {
    // 新节点为文本节点时，移除旧节点，插入新的文本节点
    if (isDef(oldCh)) {
      removeVnodes(elm, oldCh, 0, oldCh.length - 1);
    }
    api.setTextContent(elm, vnode.text!);
  }
  hook?.postpatch?.(oldVnode, vnode);
}

文本节点、只有新节点或者只有旧节点的情况都比较容易理解，而新旧节点都存在的情况，在updateChildren里面包含了整个diff的核心。

在看源代码之前，需要先明白，比较新旧节点主要目的是什么？

整个diff算法的核心就是比较新旧节点，尽可能减少DOM操作带来的开销，为了达到这个目的，需要尽可能地复用已有的旧节点。换言之

• 每个旧的子节点列表中都包含已经创建的DOM实例
• 每个新的子节点等着从已经创建的DOM实例中找到属于自己的那一个
  • 如果能找到的话，直接复用
  • 不能找到的话，才重新创建新的DOM实例
• 最后如果旧的子节点中还有未被使用的DOM实例，需要从页面移除

可见，关键思想就在于为新节点查找合适的旧节点，按照patchVnode的做法，两个vnode节点的类型相同，就可以复用他们的DOM节点。

BF版本

按照最简单的思路，遍历新节点列表，获取每个新节点的type，然后从依次从旧节点列表中找到一个符合条件的就行了呗

把问题简化，假设需要根据下面的旧列表重新构建新列表

• 旧的列表为['A','B','C','D','E']
• 新的列表为['B','A','C','F','G','D']

从上帝视角来看，先确定节点，A、B、C、D节点都存在，可以复用旧DOM；新F、新G节点需要创建；旧E节点需要移除

在只考虑实现上述需求的情况下，写一个暴力版本

var oldChildren = ['A','B','C','D','E']
var newChildren = ['B','A','C','F','G','D']

function createKeyToOldIdx(arr){
    var map = arr.reduce((acc, oldChild,index)=>{
        acc[oldChild] = index
        return acc
    },{})
    return map
}

var parentElm = oldChildren.slice()
newChildren.forEach((newChild, idx)=>{
    var map = createKeyToOldIdx(parentElm)
    var oldIdx = map[newChild]
    if(oldIdx===undefined) {
      	// 添加新节点
        parentElm.splice(idx, 0, newChild)
    }else if(oldIdx !== idx) {
      	// 移动位置
        parentElm.splice(oldIdx,1) 
        parentElm.splice(idx, 0, newChild)
    }
    console.log(idx, parentElm) 
})

// 移除不存在的节点
parentElm =  parentElm.filter(child=>{
    return newChildren.includes(child)
})
console.log(parentElm)

// 旧列表 ['A','B','C','D','E']
// 新列表 ['B','A','C','F','G','D']

// 初始parentElm与旧列表保持一致 ['A','B','C','D','E']

// 第1次循环 移动B 新的parentElm: B A C D E 
// 第2次循环 不进行操作 parentElm: B A C D E
// 第3次循环 不进行操作 parentElm: B A C D E
// 第4次循环 插入F parentElm: B A C F D E 
// 第5次循环 插入G parentElm: B A C F G D E
// 第6次循环 不进行操作 parentElm: B A C F G D E
// 第7次循环 移除旧节点 parentElm: B A C F G D 

// 最终parentElm与新列表保持一致

在这种实现方式下，

• 遍历新节点列表，查找是否存在对应的旧节点，

  • 如果存在，则调整其顺序，满足其在新节点列表中的位置；
  • 如果不存在，则创建，并插入到新节点列表的位置

• 然后移除不在新节点列表中的节点

由于parentElm会保存最新的节点顺序，因此在每轮遍历中都要通过createKeyToOldIdx查到新节点在旧列表中的位置，导致复杂度为O(mn)。

拆分子问题

因此需要对上面的算法进行改良，尽可能减少操作步骤，肉眼看起来，一种较优的做法是

• 将旧B节点移动到A节点前面，前三个节点顺序就跟新节点一致了
• 创建新F的DOM，插入到旧D前面
• 创建新G的DOM，插入到旧D前面
• 删除旧E的DOM

只需要上面4步，就可以从旧的DOM树更新成新的DOM树。了解了这个背景之后，再继续阅读源码updateChildren。将一个列表修改成另外一个列表所需要的最少操作，实际上可以参考：编辑距离，[letcode]上面也有相关的题解(https://leetcode-cn.com/problems/edit-distance/solution/bian-ji-ju-chi-by-leetcode-solution/)，其核心思路是使用动态规划，从最小的子问题触发逐步获取最优解。

参考这个思路，我们先来看看最简单的情况

["A"]
["A"]
两个列表完全相同，不需要做任何操作

["A"]
[]
删除A即可

[]
["A"]
添加B即可

["A"]
["B"]
删除A 添加B

然后再看看下面几种特殊情况

首节点或尾节点不变，这种情况下，都可以忽略相同的节点，将问题简化为连续子数组的情况，解决这种问题需要的步骤 = 解决子问题需要的步骤

["A"]
["A", "B"]
有两种拆分方式
第一种 ["A"]->["A"]子问题1和[]->["B"]的子问题2，需要操作1次
第二种 []->["A"]子问题1和["A"]->["B"]的子问题2，需要操作3次

可以看见第一种拆分方式所需要的步骤更少，则说明他可以作为最优解法

参考这种思路，拆分一下下面的问题，对于首或尾节点相同的情况

// 新增
["A", "B"];
["A", "C", "B"];
子问题 ["B"] -> ["C", "B"]
继续拆一下子问题 [] -> ["C"]

// 删除
["A", "C", "B"]
["A", "B"]
子问题 ["C"] -> []

// 修改
["A", "C", "B"]
["A", "D", "B"]
子问题 ["C"] -> ["D"]

["A","B"]
["A","C"]
子问题 ["B"] -> ["C"]

["A", "B"]
["C", "B"]
子问题 ["A"] -> ["C"]

旧首节点等于新尾节点，或者旧尾节点等于新首节点，这种情况下，只需要将新旧数组的首尾节点调整一下，就可以处理成首节点或尾节点不变的情况，解决这种问题需要的步骤 = 移动节点（1次） + 解决子问题需要的步骤

["A", "B"];
["C", "B", "A"];
先把旧节点转换成 ["B","A"]，然后再处理子问题 [""] -> ["C"]

["A", "B"]
["C", "D", "A"];
先把旧节点转换成 ["B","A"]，然后再处理子问题 ["B"] -> ["C","D"]

不满足上面情况的子问题，

["A","B"]
["C","A","B","D"]
先添加C，变成["C", "A", "B"]，然后处理子问题[]->["D"]

["A", "B"]
["C", "A", "D"]
先添加C，变成["C", "A", "B"]，然后处理子问题["B"]->["D"]

["A", "B"]
["C", "D"]
先添加C，变成["C", "A", "B"]，然后处理子问题["A", "B"]->["D"]
对于子问题，先添加D，变成["D", "A", "B"]，然后处理子问题["A", "B"]->[]

["A", "C", "B"]
["C", "D"]
原本先添加C，在添加C之前需要先查找旧节点中是否有，如果有就执行移动操作，变成["C","A","B"]->["C","D"]
处理子问题["A","B"]->["D"]，重复执行上面的过程

按照这种分治的思路，每一步我们都能将问题拆成更小的问题，那么我们可以很方便地计算出最少的操作步骤，回到上面的问题

B存在旧节点，则直接移动，前三个节点就变成一样的了，使用一步移动操作
['A','B','C','D','E']
['B','A','C','F','G','D']
操作完的DOM节点['B','A','C','D','E']

子问题,首==尾，移动一下，使用一步移动操作
['D','E']
['F','G','D']
操作完的DOM节点['B','A','C','E','D']

子问题，满足尾==尾，使用0步
['E','D']
['F','G','D']

子问题，完全不满足，则需要添加两步，移除一步
['E']
['F','G']
操作完的DOM节点
添加F ['B','A','C','F','E','D']
添加G ['B','A','C','F','G','E','D']
删除E ['B','A','C','F','G','D']

是不是比较接近我们上面提到的较优做法了？由于E节点后面会被移除，因此移动D这一步是多余的，除此之外，所需的操作与前面上帝视角观察到的基本一致。

这是很关键的一步，我们将DOM更新的问题拆分成了最小的子问题，而已经处理好的节点，他们的顺序不会再发生改变。

再来看一个比较复杂的例子，来源Snabbdom 底层Diff算法详解

首==首 || 尾==尾 ，使用0步
旧 ["A", "B", "C", "D", "E", "F", "G"]
新 ["A", "F", "E", "M", "O", "I", "E", "B", "G"]
完整DOM节点["A", "B", "C", "D", "E", "F", "G"]

子问题,首==尾 || 尾==首，需要移动位置，使用2次移动，转换成首==首 尾==尾
["B", "C", "D", "E", "F"]
["F", "E", "M", "O", "I", "E", "B"]
完整DOM节点["A", "F", "C", "D", "E", "B", "G"]

子问题，满足尾==尾，使用0步
["C", "D", "E"]
["E", "M", "O", "I", "E"]
完整DOM节点["A", "F", "C", "D", "E", "B", "G"]

子问题，完全不符合，需要4次新增和2次移除，
["C", "D"]
["E", "M", "O", "I"]
完整DOM节点
添加E ["A", "F", "E", "C", "D", "E", "B", "G"] 
添加M ["A", "F", "E", "M", "C", "D", "E", "B", "G"]
添加O ["A", "F", "E", "M", "O", "C", "D", "E", "B", "G"]
添加I ["A", "F", "E", "M", "O", "I", "C", "D", "E", "B", "G"]
移除C ["A", "F", "E", "M", "O", "I", "D", "E", "B", "G"]
移除D ["A", "F", "E", "M", "O", "I", "E", "B", "G"]

操作步骤都是类似的，接下来实现一个优化后的版本，由于没有实现insertBefore和removeChild等接口，在测试的时候需要保证每个元素唯一。

var a = ["A", "B", "C", "D", "E"];
var b = ["B", "A", "C", "F", "G", "D"];

var oldStartIdx = 0
var newStartIdx = 0
var oldEndIdx = a.length - 1
var newEndIdx= b.length - 1

var oldStart = a[0]
var oldEnd = a[oldEndIdx]
var newStart = b[0]
var newEnd = b[newEndIdx]

var parentElm = a.slice()

function createKeyToOldIdx(a) {
    var map = a.reduce((acc, oldChild, index) => {
        acc[oldChild] = index;
        return acc;
    }, {});
    return map;
}

var oldKeyToIdx = createKeyToOldIdx(a)

while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
    if(oldStart===undefined) {
        oldStart = a[++oldStartIdx]
    }else if(oldEnd === undefined){
        oldEnd = a[--oldEndIdx]
    }else if(newStart === undefined){
        newStart = b[++newStartIdx]
    }else if(newEnd === undefined){
        newEnd === b[--newEndIdx]
    }else if(oldStart === newStart) {
        oldStart = a[++oldStartIdx]
        newStart = b[++newStartIdx]
    }else if(oldEnd === newEnd){
        oldEnd = a[--oldEndIdx]
        newEnd = b[--newEndIdx]
    }else if(oldStart === newEnd){
      	// 移动到后面
        parentElm.splice(oldStartIdx, 1)
        parentElm.splice(oldEndIdx, 0, oldStart)
        oldStart = a[++oldStartIdx]
        newEnd = b[--newEndIdx]
    }else if(oldEnd === newStart){
      	// 移动到前面
        parentElm.splice(oldEndIdx, 1)
        parentElm.splice(oldStartIdx, 0, oldEnd)
        oldEnd = a[--oldEndIdx]
        newStart = b[++newStartIdx]
    }else {
        // 首尾都不满足，则查找是否有旧节点，然后从newStart开始查找
        var idxInOld = oldKeyToIdx[newStart]
        if(idxInOld===undefined){
            console.log(oldStartIdx, newStart)
            // 由于没有实现insertBefore，只能暂时获取对应的idx然后通过splice插入，
            // 否则可以直接使用在insertBefore(newStart, oldStart)直接插入节点
            let idx = parentElm.indexOf(oldStart)
            parentElm.splice(idx,0,newStart)
        }else {
            var elmToMove = a[idxInOld]
            a[idxInOld] = undefined
            parentElm.splice(idxInOld, 1)
            parentElm.splice(oldStartIdx, 0,elmToMove)
        }
        newStart = b[++newStartIdx]
    }
    console.log(parentElm)
}

if (oldStartIdx <= oldEndIdx || newStartIdx <= newEndIdx) {
    if (oldStartIdx > oldEndIdx) {
        // 批量插入新节点
        var sub = b.slice(newStartIdx, newEndIdx+1)
        var before = b[newEndIdx+1]
        // 同上，这里直接insertBefore(node, before)可以快速插入节点
        var idx = parentElm.indexOf(before)
        parentElm = [...parentElm.slice(0,idx),...sub,parentElm.slice(idx)]
    }else {
        // 批量删除无用的旧节点
        for(var i = oldStartIdx; i <= oldEndIdx;++i){
            var child= a[i]
            // 同上，这里使用node.parentNode.removeChild可以直接删除节点，而无需通过idx
            var idx = parentElm.indexOf(child)
            parentElm.splice(idx,1)
        }
    }
}
console.log(parentElm)

在这个实现中有很多个判断

• 使用新起始索引、新结束索引、新起始节点、新尾节点来结束新节点列表的子问题范围
• 使用旧起始索引、旧结束索引、旧起始节点、旧尾节点来结束旧节点列表的子问题范围
• 前四个判断是为了保证新旧节点存在，跳过undefined的节点
• 接下来的两个判断oldStart === newStart和(oldEnd === newEnd用来确定是否是旧首==新首或旧尾==新尾的情况，如果是，更新游标，直接缩小子问题范围
• 接下来的两个判断oldStart === newEnd和oldEnd === newStart用来确定是否是旧首==新尾或旧尾==新首的情况，如果是，则执行移动操作，同时更新游标，缩小子问题范围
• 最后的一个判断，用来处理常规子问题，首先检查新起始节点是否存在可以复用的旧节点
  • 如果不存在，则创建节点插入
  • 如果存在，则执行移动操作

这段代码看起来是不是很眼熟，没错，这就是updateChildren的简化版

updateChildren源码及存在的问题

现在来看updateChildren的源码，就容易理解开头的这一堆变量了。主要就是为了在每一步操作之后，所以需要操作的DOM节点范围，范围小了，需要执行的DOM操作就少，也就达到了性能优化的目的

function updateChildren(
    parentElm: Node,
    oldCh: VNode[],
    newCh: VNode[],
    insertedVnodeQueue: VNodeQueue
  ) {
    let oldStartIdx = 0;
    let newStartIdx = 0;
    let oldEndIdx = oldCh.length - 1;
    let oldStartVnode = oldCh[0];
    let oldEndVnode = oldCh[oldEndIdx];
    let newEndIdx = newCh.length - 1;
    let newStartVnode = newCh[0];
    let newEndVnode = newCh[newEndIdx];
    let oldKeyToIdx: KeyToIndexMap | undefined;
    let idxInOld: number;
    let elmToMove: VNode;
    let before: any;

    while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
      // 第一类判断，保证新旧节点存在
      if (oldStartVnode == null) {
        oldStartVnode = oldCh[++oldStartIdx]; // Vnode might have been moved left
      } else if (oldEndVnode == null) {
        oldEndVnode = oldCh[--oldEndIdx];
      } else if (newStartVnode == null) {
        newStartVnode = newCh[++newStartIdx];
      } else if (newEndVnode == null) {
        newEndVnode = newCh[--newEndIdx];
       // 第二类判断，起始或末尾节点是否相同
      } else if (sameVnode(oldStartVnode, newStartVnode)) {
        patchVnode(oldStartVnode, newStartVnode, insertedVnodeQueue);
        oldStartVnode = oldCh[++oldStartIdx];
        newStartVnode = newCh[++newStartIdx];
      } else if (sameVnode(oldEndVnode, newEndVnode)) {
        patchVnode(oldEndVnode, newEndVnode, insertedVnodeQueue);
        oldEndVnode = oldCh[--oldEndIdx];
        newEndVnode = newCh[--newEndIdx];
      } else if (sameVnode(oldStartVnode, newEndVnode)) {
        // 第三类判断，首尾节点是否相同，执行移动操作
        // Vnode moved right
        patchVnode(oldStartVnode, newEndVnode, insertedVnodeQueue);
        api.insertBefore(
          parentElm,
          oldStartVnode.elm!,
          api.nextSibling(oldEndVnode.elm!)
        );
        oldStartVnode = oldCh[++oldStartIdx];
        newEndVnode = newCh[--newEndIdx];
      } else if (sameVnode(oldEndVnode, newStartVnode)) {
        // Vnode moved left
        patchVnode(oldEndVnode, newStartVnode, insertedVnodeQueue);
        api.insertBefore(parentElm, oldEndVnode.elm!, oldStartVnode.elm!);
        oldEndVnode = oldCh[--oldEndIdx];
        newStartVnode = newCh[++newStartIdx];
      } else {
        // 第四类判断，根据key找到可以复用的DOM节点
        if (oldKeyToIdx === undefined) {
          oldKeyToIdx = createKeyToOldIdx(oldCh, oldStartIdx, oldEndIdx);
        }
        idxInOld = oldKeyToIdx[newStartVnode.key as string];
        if (isUndef(idxInOld)) {
          // 如果没有可复用的节点，就重新创建新节点
          api.insertBefore(
            parentElm,
            createElm(newStartVnode, insertedVnodeQueue),
            oldStartVnode.elm!
          );
        } else {
          // 如果有可复用的节点，则执行移动操作
          elmToMove = oldCh[idxInOld];
          if (elmToMove.sel !== newStartVnode.sel) {
            api.insertBefore(
              parentElm,
              createElm(newStartVnode, insertedVnodeQueue),
              oldStartVnode.elm!
            );
          } else {
            patchVnode(elmToMove, newStartVnode, insertedVnodeQueue);
            oldCh[idxInOld] = undefined as any;
            api.insertBefore(parentElm, elmToMove.elm!, oldStartVnode.elm!);
          }
        }
        newStartVnode = newCh[++newStartIdx];
      }
    }
    if (oldStartIdx <= oldEndIdx || newStartIdx <= newEndIdx) {
      if (oldStartIdx > oldEndIdx) {
        // 旧节点被消耗完毕，新节点还有剩余，则都执行插入操作
        before = newCh[newEndIdx + 1] == null ? null : newCh[newEndIdx + 1].elm;
        addVnodes(
          parentElm,
          before,
          newCh,
          newStartIdx,
          newEndIdx,
          insertedVnodeQueue
        );
      } else {
        // 反之，新节点被消耗完毕，旧节点还有剩余，都执行移除操作
        removeVnodes(parentElm, oldCh, oldStartIdx, oldEndIdx);
      }
    }
  }

按照上面的分析，在移动节点这一步，其实并不是最优的，由于删除无用节点的操作都是在最后执行的，在上面

['A','B','C','D','E']
['B','A','C','F','G','D']

的例子中，会先移动D到E后面，然后再把E删除，这一步无疑是无用的。由于被删除的节点并不影响整个diff，一种可行的方式是调整代码顺序，提前删除

• 先遍历新旧节点，提前移除不会用到的节点，这里会多执行一轮循环，之后的问题可以简化为['A','B','C','D'] -> ['B','A','C','F','G','D']
• 再进行上述的diff操作
• 最后在newStartIdx <= newEndIdx时插入未被处理的vnode

是否采用这种方案主要取决于多执行一轮循环用于删除无用节点得到的性能提升是否比减少一轮循环，使用可能带来的额外的移动操作得到的性能提升更大，但很显然，Snabbdom和Vue都没有采用这种提前删除无用节点的方案。

了解了内部的实现之后，我们再回答上面刻意避免的一个问题：vnode.key的作用是什么?

在sameVnode可以看见

function sameVnode(vnode1: VNode, vnode2: VNode): boolean {
  const isSameKey = vnode1.key === vnode2.key; // 都为undefined或者字符串相等
  const isSameIs = vnode1.data?.is === vnode2.data?.is;
  const isSameSel = vnode1.sel === vnode2.sel;

  return isSameSel && isSameKey && isSameIs;
}

key的一个作用是用来判断两个vnode是否相同，参与到上面diff过程的一些判断中，在都不定义key的情况下，两个相同sel的vnode会返回true，也就是常说的就地复用，只会更新DOM相关的信息，而不参与移动操作

在createKeyToOldIdx中可以查看定义了key的情况

function createKeyToOldIdx(
  children: VNode[],
  beginIdx: number,
  endIdx: number
): KeyToIndexMap {
  const map: KeyToIndexMap = {};
  for (let i = beginIdx; i <= endIdx; ++i) {
    const key = children[i]?.key;
    // 不处理undefined
    if (key !== undefined) {
      map[key as string] = i;
    }
  }
  return map;
}
// 根据key返回旧节点的索引值
idxInOld = oldKeyToIdx[newStartVnode.key as string];
if (isUndef(idxInOld)) {
  // ...创建新节点
}else {
  // ... 移动操作
}

如果定义了key，则会在旧列表中找到对应的DOM节点，然后执行移动操作；换句话说，key用来在一个兄弟节点列表中进行唯一标记，这样在构建新节点的时候，会根据key去查找已经存在的节点，而不是就地复用，同时移除key不存在的节点。

举个例子

在不使用key的时候，将[h('div', {}, '1'),h('div', {}, '2')]修改为[h('div', {}, '2'),h('div', {}, '1')]，会将第一个DOM的文本节点修改为'2'，而不是移动两个DOM节点的顺序，这在DOM节点比较简单的时候貌似更加高效

在使用key的时候，[h('div', {key:'1'}, '1'),h('div', {key:'2'}, '2')]修改为[h('div', {key:'2'}, '2'),h('div', {key:'1'}, '1')]，会根据第一个新节点的key(这里是'2')去旧节点列表中查找，找到对应的DOM节点（第2个DOM节点），然后执行位置移动操作，对于简单文本的改动，貌似是不划算的；但如果这两个节点的子节点是比较复杂的内容，交换顺序就比较划算了。

总结一下

• 不使用key，尽可能就地复用已存在的同类型DOM
• 使用key，基于key的变化查找旧的节点，修改顺序进行移动操作，同时查出key不存在的元素

通过Module处理不同的DOM属性

内置模块Module包含一些钩子方法，在vnode节点执行create、update、remove等操作时，会传入新旧的vnode然后执行，然后在新旧vnode的DOM实例上进行一些操作

export type Module = Partial<{
  pre: PreHook;
  create: CreateHook;
  update: UpdateHook;
  destroy: DestroyHook;
  remove: RemoveHook;
  post: PostHook;
}>

以classModule为例

function updateClass(oldVnode: VNode, vnode: VNode): void {
  let cur: any;
  let name: string;
  const elm: Element = vnode.elm as Element;
  // `VNodeData`上支持传入`class`字段，类似于`{ class: { active: true, selected: false } }`，为`true`表示添加样式类，为`false`表示移除样式类
  let oldClass = (oldVnode.data as VNodeData).class;
  let klass = (vnode.data as VNodeData).class;

  if (!oldClass && !klass) return;
  if (oldClass === klass) return;
  oldClass = oldClass || {};
  klass = klass || {};
  // 从新的DOM实例上移除旧的样式类
  for (name in oldClass) {
    if (oldClass[name] && !Object.prototype.hasOwnProperty.call(klass, name)) {
      // was `true` and now not provided
      elm.classList.remove(name);
    }
  }
  // 添加或移除新的样式类
  for (name in klass) {
    cur = klass[name];
    if (cur !== oldClass[name]) {
      (elm.classList as any)[cur ? "add" : "remove"](name);
    }
  }
}

export const classModule: Module = { create: updateClass, update: updateClass };

在init时，会解析传入的内置模块，并将其通过闭包放在cbs变量中，在patch时的对应时机，就可以调用相关方法，传入新旧vnode，处理真实的DOM属性

  const cbs: ModuleHooks = {
    create: [],
    update: [],
    remove: [],
    destroy: [],
    pre: [],
    post: [],
  };

  const api: DOMAPI = domApi !== undefined ? domApi : htmlDomApi;

  for (i = 0; i < hooks.length; ++i) {
    cbs[hooks[i]] = [];
    for (j = 0; j < modules.length; ++j) {
      const hook = modules[j][hooks[i]];
      if (hook !== undefined) {
        (cbs[hooks[i]] as any[]).push(hook);
      }
    }
  }

这种设计可以避免在diff的时候关注相关的DOM操作细节，还有很有意思的。

小结

本文虽然命名为Snabbdom源码分析，但实际上主要只关注了patch相关的流程

• 初始化时，使用newVnode，在createElm时通过前序遍历构建DOM树
• 更新时，对于不同类型的oldVnode和newVnode，先根据newVnode创建新DOM树，然后移除旧的oldVnode
• 更新时，对于相同类型的oldVnode和newVnode进行patchVnode操作
  • 只存在旧子节点列表，执行移除操作
  • 只存在新子节点列表，执行添加操作
  • 同时存在且两者不相同，则执行updateChildren操作，其中包含了diff算法的实现
• diff算法的核心思路是通过分治的思想，在每一步操作之后缩小需要检测的范围

Snabbdom的实现十分精简，是一份非常值得阅读的源码。现在在回头去看Vue的源码，就轻松得多了。React在使用Fiber之后，摒弃了递归diff的做法，但其diff的核心思想是类似的，接下来可以重新阅读一下React的diff实现了。

相关参考

• Snabbdom 底层Diff算法详解
• 虚拟DOM算法库-Snabbdom

#snabbdom #diff

你要请我喝一杯奶茶？

版权声明：自由转载-非商用-保持署名和原文链接。

本站文章均为本人原创，参考文章我都会在文中进行声明，也请您转载时附上署名。